When will I get the cards I want in Pokemon TCG Pocket

When Pokemon first took the world by storm, I was 8 years old. Which is to say, I was the perfect age for it. And I was WAY into it.

Nearly 30 years later, and something of it is still deeply ingrained in my psyche. So when Pokemon TCG Pocket was released, I was an easy mark.

Secret Mission

Garchomp is my favourite Pokemon, so when the second expansion — Space Time Smackdown — was release with a full-art Garchomp, I had to have it.

And I got it!

But then I learned about secret mission: Champion of the Sinnoh Region

Completing this mission would earn me a Garchomp emblem, to proudly display on my player profile.

How hard could it be?

To complete the secret mission, I would need to collect:

• Garchomp (one star)
• Lucario (one star)
• Gastrodon (one star)
• Spiritomb (one star)
• Cynthia (two star)

Luckily, by that point I already had the Garchomp and Lucario, so I only needed 2 more one star cards and a two star card to complete the mission.

Getting cards

There are four ways to acquire a given card

1. pull it from a booster pack
2. wonder pick it
3. trade for it
4. buy it with pack points

We’ll come back to (1)

Wonder Pick

Wonder pick shows you sets of cards that other players pulled when opening a booster pack. You can chose a set, and the cards from that set are placed face-down and shuffled. You then pick one, and get a copy of whatever is revealed.

There are 5 cards to pick from, which means a 1 in 5 chance of getting the card you want, which is much better odds than pulling the card from a booster pack.

However, this only works if the card you want is available to pick at all. This becomes less and less likely over time, as new expansions are released and players open fewer boosters from the older expansions.

For that reason, this method is too unreliable to take into account.

Trade

The trade feature is trash, and we won’t dignify it with further discussion.

Pack Points

With each booster pack you open, you earn 5 pack points (pp), and with enough pack points you can out-right buy the card you want.

The number of points required to buy a card depends on its rarity. In my case, the relevance numbers are

• one star: 400 pp
• two star: 1250 pp

So all together, I would need… 2050 pp.

To achieve that many pack points, I would need to open 410 booster packs. Let’s put that in context.

If you’re a free-to-play player, you get to open 2 booster packs a day. That means it would take 205 days to get the required number of points, or almost 7 months!

If, instead, you pay for a premium pass (£7.99/month), you get to open a third pack per day, bringing it down to 137 days or about 4.5 months.

It’s not impossible, but it would suck the joy out of the game; always opening packs from the same expansion, and in most cases getting low value duplicates over and over.

There are various missions and bonuses which allow you to open more booster packs per month, but not enough to move the needle much.

Cold hard cash

What if you wanted to buy the booster packs with real money?

The best deal just now is to buy the 690 Pokemon gold bundle (500 paid + 190 ‘free’) for £79.99.

One booster pack costs 6 gold, so the bundle would give you 115 booster packs at a cost of about 69.5p per pack.

So, to open the 410 booster packs, I would have to pay £285 !

Yeah. That’s a lot of money to spend on an imaginary object.

Booster Packs

But wait, let’s go back to point (1).

Sure, pack points are a guaranteed way to get the cards you want, but if you’re opening 410 booster packs, that’s ample opportunity to just pull some of those cards. Right?

Offering Rates

Helpfully, the game shares it’s “offering rates” — the probability of pulling each card.

So, what’s the probability of getting one or more of the desired cards when opening 410 booster packs?

The relevant offering rates break down like so:

• each booster pack contains 5 cards
• in regular booster packs
  • the first 3 cards are always one diamond ‘common’ cards, so we can ignore them
  • for the 4th card
    • one star - 0.214%
    • two star - 0.041%
  • for the 5th card
    • one star - 0.857%
    • two star - 0.166%
• the probability of opening a ‘rare’ booster - 0.05%
  • in a rare booster there are 5 rare cards
  • all rare cards (including one and two star) have the same probability - 3.846%

Note, these offering rates apply to the Space Time Smackdown booster packs. Other expansions may have different rates.

Pull probabilities

Let’s start by looking at the probability of pulling a one star card from a regular booster

It’s easiest to calculate the probability of NOT pulling the card (not card 4 and not card 5), then subtract from 1

p(one star) = 1 - (1 - p(one star|4)) * (1 - p(one star|5))
            = 1 - (1 - 0.00214) * (1 - 0.00857)
            = 0.0107

Calculated the same way, the two star probability is p(two star) = 0.00207

For rare booster packs, there are 5 opportunities for pulling a given card, with the same probability each time, and a card may appear more than once

p(rare) = 1 - (1 - 0.0384) ^ 5
        = 0.178

The probability is the same for both one and two star cards.

Combining the probabilities for rare and regular boosters, we get

P(one star) = 0.0108
P(two star) = 0.00216

Opening boosters

We want to know the probability of pulling one or more copies of a card while opening a large number of booster packs

As before, it’s easiest to come at it via the probability of not pulling the card in any booster

p(card, N) = 1 - (1 - p(card)) ^ N

As previously mentioned, I would have to open N = 410 booster packs to get the required number of pack points, so we have

p(one star, 410) = 0.988
p(two star, 410) = 0.588

In other words, I’m almost certainly going to pull one or both of the one star cards, but the two star card is only slightly better 50:50

The probability of pulling all three is 58.7%

But, if I do pull a one star card, I won’t need to buy it with pack points, so then don’t need to open as many boosters. But opening fewer boosters decreases the probability of pulling the card. Is there some sweet spot?

Simulation

How many boosters should I expect to open before I either pull all the cards, or else have enough points to buy the cards I haven’t pulled yet?

This is more difficult to calculate from pure probability, so I used a simulation instead — source code here.

The results looks like this

# Average boosters opened - 205.0471

# Most likely number opened - 250 (0.5076)
# Probability above most common - 0.0789

# Average copies of each card
 - Cynthia: 0.4393
 - Spiritomb: 2.2016
 - Gastrodon: 2.2031

# Probabilities of card sets
 - Cynthia: 0.0116
 - Spiritomb: 0.0137
 - Gastrodon: 0.0159
 - Cynthia, Spiritomb: 0.0925
 - Cynthia, Gastrodon: 0.0928
 - Cynthia, Gastrodon, Spiritomb: 0.2265
 - Gastrodon, Spiritomb: 0.547

I should expect to open ~205 booster packs before getting all three cards.

The most likely outcome is I’ll pull the 2 one stars and will have to buy the two star, with probability about 50%. The probability of having to open more than 250 packs is only 7.89%

There’s roughly a 1 in 5 chance of pulling all 3 cards before getting to the required pack points. The probability of pulling none of the cards is so unlikely it didn’t happen in 10,000 simulations (but it’s not impossible).

If we plot a histogram, we get a clearer picture of what’s going on

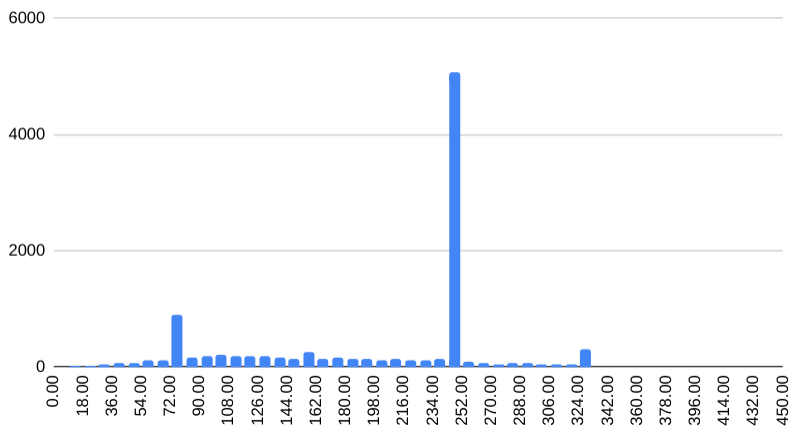
There are four clear peaks corresponding to 80, 160, 250, and 330 packs — or 400 pp, 800pp, 1250 pp, and 1650 pp. Those numbers should look familiar.

Head start

When I starting this mission I had already opened about 100 boosters (500 pp).

Taking that into account, the results become

# Average boosters opened - 142.9071

# Most likely number opened - 150 (0.4728)
# Probability above most common - 0.2493

# Average copies of each card
 - Cynthia: 0.3124
 - Gastrodon: 1.5405
 - Spiritomb: 1.5657

# Probabilities of card sets
 - (none): 0.0007
 - Spiritomb: 0.0464
 - Gastrodon: 0.0482
 - Cynthia: 0.056
 - Cynthia, Gastrodon, Spiritomb: 0.078
 - Cynthia, Gastrodon: 0.0826
 - Cynthia, Spiritomb: 0.0911
 - Gastrodon, Spiritomb: 0.597

Now the expected number of boosters is 145. Adding that to the 100 I already opened comes to 245, which is more than the expected number when starting from zero.

But as before, I will most likely have to buy the two star card with pack points, and it’s highly likely that I will pull the one star cards in the meantime.

Gotta catch ‘em all

In case you were wondering, the expected number of packs to get all 5 Champion of Sinnoh cards is 215 (1075 pp), which is much less than the 2850 pp required to buy the cards. It’s less even than the cost of just the two star card.

But that calculation isn’t quite correct — Lucario is only available in the Space Time Smackdown Dialga boosters, while the rest are in Palkia. That means, if we only open Palkia boosters, there’s zero chance of pulling Lucario.

Figuring out the optimal strategy in that case is left as an exercise for the reader.

Conclusion

No matter how we come at the calculation, the most likely outcome is that I’ll have to buy the two star Cynthia with pack points, but there’s a good chance of pulling the one star cards. This comes down to two star cards being much rarer than one star cards; the probability of pulling Cynthia in any given pack is only about 1 in 500.

Since I started drafting this post, I’ve gotten up to 900 pack points, and I managed to pull one of the one star cards (Spiritomb) along the way.

Re-running the simulation, the expected number of boosters in now down to 85.

Still some way to go…

Chris.

Oh, and if you want to add me, my user name is ‘oatzy’ and my friend code is 0625-2776-5308-5489

I’m too much of a coward for Versus battles (PvP), but if you offer me a trade I will offer you something in return, even if I don’t need what you offered.