Any Probability with a Dice or Coin

I woke up from a dream with a question in my head – can we generate any probability with a coin and a six-sided dice?

Let’s focus on the dice - what probabilities can we generate with a dice roll?

• 1 in 6 is easy, if you roll a 1 you win
• for 1 in 2, if the result is even – 2, 4, or 6 – you win
• for 1 in 3, if the result is divisible by three – 3 or 6 – you win
• 1 in 4 is less obvious, but since 1/4 = 1/2 * 1/2, we can roll the dice twice and win if both rolls come up even.

But what about 1 in 5 ?

Keep rollin’ rollin’ rollin’ rollin’

Let’s start by stubbornly pretending that the dice only has five side.

• If you roll a 1, you win.
• If you roll 2, 3, 4, or 5, you lose.

Problem solved.

But wait! What if you roll a 6?

In that case, let’s try rolling again – same rules apply – and keep rolling until we win or lose.

What’s the probability of winning?

• the probability of winning – rolling a 1 – on the first roll is p(1) = 1/6
• the probability of winning on the second roll is the probability of rolling a 6 on the first roll (1/6) multiplied by the probability of rolling a 1 on the second roll (1/6)
  • p(2) = 1/6 * 1/6 = 1/36
  • the probability of winning on first OR second roll is the sum of the probabilities
    • p(1||2) = p(1) + p(2) = 1/6 + 1/36 = 0.19444..
• the probability of winning on the third roll, following the same logic, is
  • p(3) = 1/6 * 1/6 * 1/6 = (1/6)^3 = 1/216
  • the probability of wining on the first, second, or third roll is then
    • p(1||2||3) = 1/6 + 1/36 + 1/216 = 0.19907..

This is looking promising – the probability is getting closer and closer to 0.2 (= 1/5)

So, the probability of winning at all, in any round, is the sum of the probabilities of winning on any of a potentially infinite number of rounds

p = p(1) + p(2) + p(3) + ... p(i) + ... + p(inf)

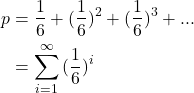
This a a geometric series, for which there’s a simple formula

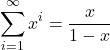
And substituting x = 1/6 we get… p = 1/5

tada!

Granted, this approach could result in rolling dice forever, without ever winning or losing (by rolling infinite 6s). But the probability of that happening is diminishingly small; the probability of rolling just four 6s in a row is less than 1%

Roll again

Now, we might well wonder: Was this a fluke? Or does this work for other numbers?

Let’s try for 1 in 4.

• roll 1 -> win
• roll 2, 3, or 4 -> lose
• roll 5, or 6 -> re-roll

The probability is calculated the same as before

• the probability of winning – rolling a 1 – on the first roll is p(1) = 1/6
• the probability of winning on the second roll is the probability of a re-roll (2/6 = 1/3) multiplied by the probability of winning on the second roll (1/6)
  • p(2) = 1/6 * 1/3
• the probability of winning on the third roll is p(3) = 1/6 * 1/3 * 1/3 = 1/6 * (1/3)^2
• and so on

Adding up, this time, we have

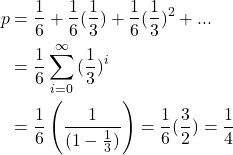
Just like we wanted.

[NOTE: this time, the sum is from i=0 rather than i=1]

Prove it

And since we’re on a roll (pun intended), let’s see if this always works.

Suppose we have a dice with N sides, and we want to roll for a 1/r probability, with integer r <= N

Probability of a re-roll is

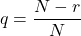
And following through the same logic as before

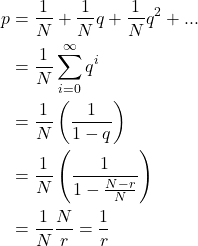
QED

Can you take me higher

So with our six-sided dice, we can get probabilities for 1/2 to 1/6. But what about 1/7?

Our algorithm only lets us represent probabilities 1/r for integer r <= N, where N=6 for a standard six-sided (d6) dice.

Sure, we could go up to a dice with more sides, like an octahedral (d8). But I don’t have one of those.

How about this – roll the d6 dice twice; each roll represents a digit in a two-digit, base-6 number.

We’ll treat 6 as zero. So if we roll [2][5] we have hexary (sexary?) number 25 = (2*6) + 5 = 17 in decimal

Now we can represent 36 values. Can you see where this is going?

So we roll our dice twice

• if the result is two 6s – [0][0] = decimal 0 – then we win
• if the result is decimal 1 to 6 – hexary [0][1] to [1][0] – we lose
• otherwise, re-roll.

As previously demonstrated, we know this will converge on 1/7. Job done.

Is this practical? Not really. The re-roll probability in this case is 29/36 ~ 80%, which means potentially a lot of re-rolls.

But, it does work.

Great expectations

Actually, how many rolls would we expect?

We can think of rolling and re-rolling as a Bernoulli trial, where the probability of the trials ending (not re-rolling) is given by p(end) = 1 - q = r/N

The expected number of trials is then given by T = 1/p(end) = N/r

For the two dice 1/7 example, that comes out to 36/7 = 5.1428.. rolls (or 10.28.., since we’re rolling two dice for each trial).

By comparison, the single dice 1/5 probability would expect only T = 6/5 = 1.2 rolls

We can get an improvement on two dice for 1/7 by instead pairing the dice with a coin – flip a coin for the first digit and roll a dice for the second. This gives us 12 possible values and means we expect only 12/7 = 1.714.. trials (rolls and flips), which is much more reasonable.

Flippin’ heck

There’s question that had been floating around in my head for a while, before the dream – can we get a probability of 1 in 3 with one or more coin flips?

Following the same algorithm as for the dice, we can flip two coins (or one coin twice). The result is interpreted as a two digit binary number – heads = 0, tails = 1, giving us 4 possible values.

• If we get two heads – (0)(0) – we win!
• If we get one head and one tail – (0)(1) or (1)(0) (1 or 2 in decimal) – we lose.
• If we get two tails – (1)(1) (decimal 3) – flip again.

Repeat until the game ends. Surprisingly simple.

The expected total number of coin flips is 2 * N/r = 2 * 4/3 = 2.66..

So there you go - you can generate any probability with a single dice or coin.

Wait, why are we only half way through this post?

Re-numeration

All the probabilities we’ve looked at so far have been one-in-X. What about higher numerators? Can we get 2-in-5 with a dice?

If the trick worked for 1/5, why not 2/5?

• roll a 1 or 2 -> win
• roll 3, 4, 5 -> lose
• roll 6 -> re-roll

Now

• the probability of winning on the first roll – rolling 1 or 2 – is p(1) = 2/6 (= 1/3)
• the probability of a re-roll is 1/6, so the probability of winning on the second roll is p(2) = 1/6 * 1/3

You should know the words by now

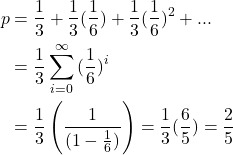
Likewise, if we have an N sided dice and want probability p = a/b, where integers 0 <= a < b <= N

The probability of winning on the first roll is a/N and the probability of a re-roll is q = (N - b) / N

So the total probability of winning is

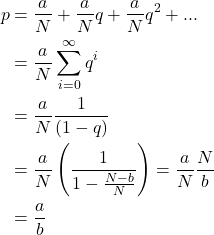
QED again.

Okay, now we’ve covered everything. Right?

Stop making sense

“But wait…“, you say, “what about irrational probabilities?”

“Oh…“, I say, “right…“ :/

An irrational probability would be something like 1/pi or 1/e. Can we roll that with a six-sided dice?

So far, we’ve been assuming the probabilities are the same each round – for example, if we roll a 1 we win, if we roll a 6 we re-roll, regardless of how many rolls we’ve already thrown.

What if we change things up. Let’s stick with re-rolling when we get a 6, but vary the win condition on each round.

For example, suppose we did the following

• if we roll 1 on the first round we win
• if we roll 1, 2, 3, 4, or 5 on the second round we win
• if we roll 1 or 2 on the third round we win
• and so on

The probability is then

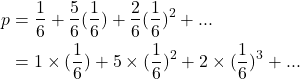
And we can see this inching upwards

p(1)          = 0.1666..
p(1||2)       = 0.3055..
p(1||2||3)    = 0.3148..
p(1||2||3||4) = 0.3179..
...

towards p = 0.3183... = 1/pi

All your base

We can generalise this approach like so – we have an N sided dice, and to win on the i-th throw, we need to roll ai or lower, where ai is an integer 0 <= ai < N

The total probability of winning is then

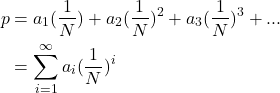
And what we’re describing here is actually the base-N representation of p. It’s correct by construction, so no proof required.

The coefficients ai can be calculated like so

def tobase(p, N):
    while p > 0:
        a, p = divmod(p * N, 1)
        yield int(a)

# list(itertools.islice(tobase(1/math.pi, 6), 10))

(for p < 1)

So, for example, the first 10 values of ai for 1/pi in base-6 are

1, 5, 2, 4, 3, 1, 0, 2, 2, 1, ...

and for 1/e in base-6

2, 1, 1, 2, 4, 3, 4, 4, 1, 1, ...

The same works for coin flips as well – 1/pi in base-2 is

0, 1, 0, 1, 0, 0, 0, 1, 0, 1, ...

Is this practical – memorising an infinite sequence of coefficients? Almost certainly not.

Sixes and sevens

Incidentally, this approach does also works for rational numbers.

And it gives us an interesting, alternative way of getting 1/7 from a dice roll.

The coefficients (ai) for 1/7 in base 6 are

0, 5, 0, 5, 0, 5, 0, 5, 0, 5, ...

alternating 0 and 5

In terms of dice rolls, 0 means we lose if we roll anything other than 6 (re-roll), and 5 means we win if we roll anything other than 6

This translate to:

• Roll the dice until you get anything other than 6
• If you rolled an odd number of times, you lose.
• If you rolling an even number of times, you win.

For example, if you rolled 6, 6, 3, then you stopped on the third roll, which is odd, so you lose. Sorry.

But if you rolled 6, 1, that’s an even number of rolls, so you win. Woo!

This is much easier to comprehend than the previously discussed 1/7 methods, and it has an expected number of rolls T = 6/5 = 1.2. So it would be my preferred method.

There’s a similarly nice, repeating pattern for 1/7 in base 2

0, 0, 1, 0, 0, 1, 0, 0, 1, ...

This means we can flip a coin until we gets a heads, and if the number of flips was divisible by 3, we win.

Back to dreaming

Now are we done?

What about imaginary numbers? Can we do imaginary probabilities?

…

Merry Christmas.

Chris.

[yes, I know the singular of ‘dice’ is ‘die’]