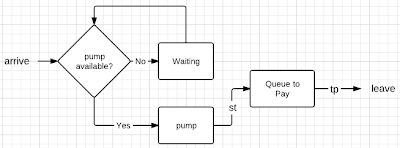
Quick Look: Petrol Station Model

23 Jan 2011 So a model of a petrol station is effectively the same as the café (albeit with different variables), EXCEPT that for the petrol station you queue to pay just before you leave (rather than as soon as you arrive).

And what this specifically means is that a pump is occupied for the time it takes to fill the car, PLUS the time it takes to queue to pay. But at the same time, the queue has a maximum size - i.e. if all the pumps are occupied and all the owners are in line to pay.

Interestingly, a barriered car park is around about the intersection of the café and the petrol station (in modeling terms). But that's a whole other story.

For simplicity, we can assume that all pumps have both diesel and petrol, and that there's an equal chance that any given car's petrol tank is on either the left or the right side of the car. That's not to say you couldn't factor in these things, if you were so inclined, but their effects would average out over multiple simulations.


Of course, it doesn't take a mathematical model to tell you that the control of flow comes down, primarily, to how quickly people are able to pay for their petrol. Which is why "pay at the pump" is so useful - it removes the queuing part of the model.

But what the model can tell you is how quickly the staff need to work to limit backlogs; basically, they have to serve quicker than the average arrival rate.

Like with the café model you could probably adapt this model to predict how long you can expect to wait as well. And as a final, intellectual, exercise, you could factor in pay at the pump (assuming not everyone who can, does), and look at to what degree that allows the staff to relax their pace.

Here's an example output graph,
Blue is pumps in use, yellow is number of people queuing to pay and orange is waiting for a pump.

You can find the code here if you're interested.


Oatzy.