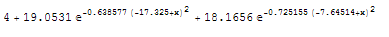Rush Hour

30 Dec 2010 So this ultimately turned out to be more an exercise in practicing fitting functions to data. But nonetheless, here it is.

I was browsing the Department of Transport website (as you do) looking for data for the whole trains thing. I didn't find what I was looking for, but I did find this
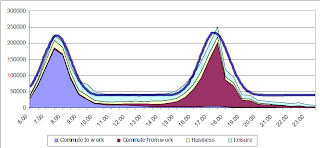
This is, "Passenger numbers: by time of departure from station", and "represents rail travel in Great Britain as a whole, on an average weekday outside of school holidays". The bottom one is a breakdown by purpose of being on the train; the top on is total numbers.

So the first thing you notice is there are curves for commuters going to and coming back from work - rush-hours. Now I'd thought that there would be a minor peak around midday, but apparently not.

So if you wanted to get an approximate model of this graph, the first place you'd probably start would be notice that the commuters' curves are fairly 'normal' (in the mathematical sense.

So working on them separately, and using Mathematica's FindFit function you get your curves. You then combine them and adjust them upwards to include business/leisure and you get this
Which is acceptable - it fits the first half better than the second. But not amazing overall. The equation is this, for those interested
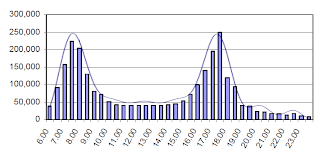
So just for the hell of it, I tried getting a better fit using a Fourier series. This time using the totals, and again, this was using Mathematica. But for a Fourier series you're combining Sines and Cosines.

The accuracy of the fit depends on how many terms you include. I tried various iterations until I found the most acceptable fit with the fewest terms, and that looks like this
Which in all fairness is a pretty good fit. Except for that it's got 15 terms and looks like this
Not what you would call elegant.

So that's that. I doubt anyone's actually interested, but for all the effort I put in to it, I thought it worth 'formally' writing it up. Otherwise it'd be lost forever somewhere on my laptop and in one of my various notebooks.

The other thing is, it could come in handy with the train problem. But that's a whole other story.

Anyway, I'm starting to ramble, so lets just leave it at that.


Oatzy.